Xin chào các bạn! Hôm nay chúng ta sẽ cùng nhau khám phá về một kiến thức vô cùng thú vị – thuật toán Qui Hoạch Động. Đây là một phần quan trọng trong lĩnh vực thuật toán và chúng ta hãy tìm hiểu những điều bổ ích về nó.
Giới thiệu về thuật toán Qui Hoạch Động
Thuật toán Qui Hoạch Động là một kỹ thuật thiết kế thuật toán tuyệt vời, cho phép chia nhỏ bài toán lớn thành các bài toán nhỏ hơn. Chúng ta sẽ sử dụng lời giải của các bài toán nhỏ để tìm lời giải cho bài toán ban đầu.
Khác với phương pháp Chia để Trị, thuật toán Qui Hoạch Động tính toán trước lời giải của các bài toán con và lưu trữ chúng vào bộ nhớ (thường là một mảng). Sau đó, chúng ta sẽ sử dụng lời giải đã tính toán trước đó để giải quyết bài toán lớn hơn.
Ví dụ: Hãy cùng xem một bài toán kinh điển sử dụng Qui Hoạch Động – bài toán Fibonaci. Chúng ta sẽ tính số Fibonaci thứ n, ký hiệu F(n).
- F(0) = 0, F(1) = 1.
- F(n) = F(n-2) + F(n-1) với n > 1.
- Ví dụ: F(2) = 1, F(3) = 2, F(4) = 3, F(5) = 5, F(6) = 8…
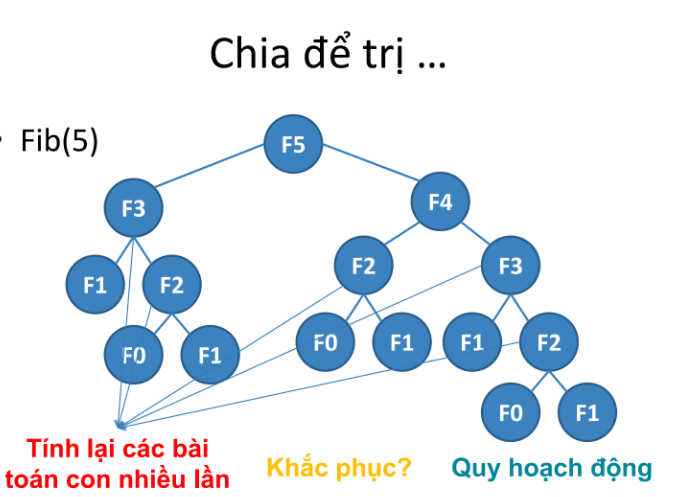
Để giúp các bạn hiểu rõ hơn về Qui Hoạch Động, chúng ta sẽ so sánh nó với phương pháp Chia để Trị.
Chia để Trị và Qui Hoạch Động
function Fib(n) {
if n < 2 then return n;
else return Fib(n-1) + Fib(n-2);
}Chúng ta thấy rằng phương pháp Chia để Trị yêu cầu tính toán lại các bài toán con rất nhiều lần. Điều này không hiệu quả cho lắm.
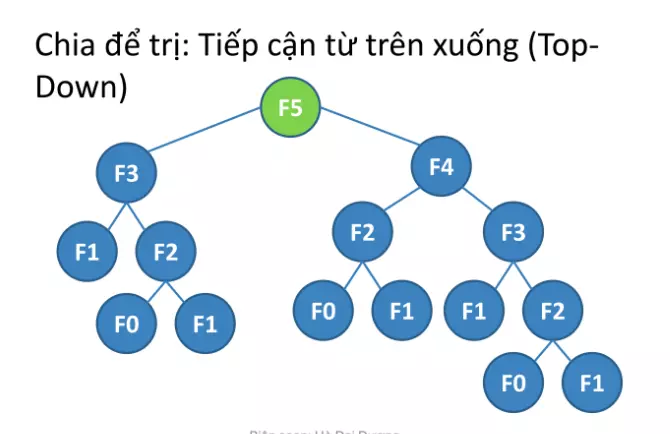
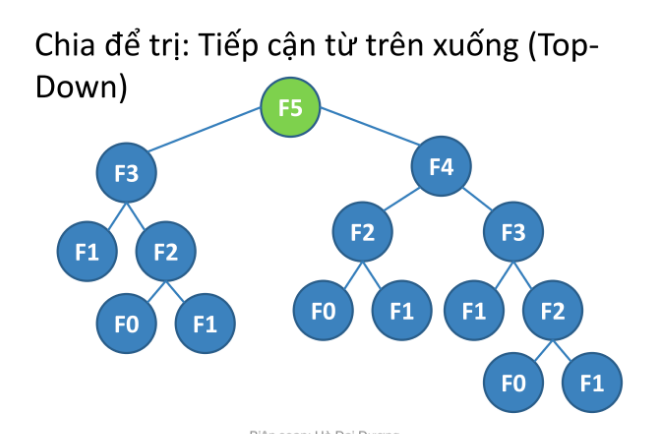
Vậy, hãy cùng nhìn vào Qui Hoạch Động và xem nó hoạt động như thế nào.
Phân tích thuật toán Qui Hoạch Động
Qui Hoạch Động sử dụng một mảng để lưu trữ kết quả của các bài toán con. Điều này giúp quá trình tính toán trở nên đơn giản hơn rất nhiều.
Một điều thú vị là tốc độ và bộ nhớ là hai yếu tố tương đương nhau. Trong bài toán này, tốc độ tính toán tỉ lệ nghịch với bộ nhớ (RAM). Dùng Qui Hoạch Động sẽ tối ưu hơn khi tính toán với những con số lớn, có thể lên đến triệu hoặc tỉ. Dùng phương pháp Chia để Trị để tính F[1 tỷ] chẳng hạn, máy tính của bạn có thể treo đấy. Hãy thử nếu bạn không tin!
Tóm lại, qui hoạch động hoạt động theo các bước sau:
- Phân rã: Chia bài toán cần giải thành những bài toán con nhỏ hơn, có thể giải trực tiếp hoặc không.
- Giải các bài toán con và ghi nhận lời giải: Lưu trữ lời giải của các bài toán con vào một bảng để sử dụng lại.
- Tổng hợp lời giải: Tổng hợp lời giải các bài toán con kích thước nhỏ hơn thành lời giải bài toán lớn hơn. Tiếp tục cho đến khi thu được lời giải của bài toán gốc.
Kết luận
Cuối cùng, bạn đã hiểu cơ bản về thuật toán Qui Hoạch Động rồi đấy. Nhưng hãy kiên nhẫn, đây chỉ là phần đầu để bạn có cái nhìn tổng quan về nó. Trong phần tiếp theo, chúng ta sẽ khám phá những bài toán phức tạp hơn và áp dụng Qui Hoạch Động vào chúng. Hãy luôn theo dõi để không bỏ lỡ nhé!
Dnulib.edu.vn sẽ cung cấp cho bạn thêm kiến thức bổ ích về Qui Hoạch Động và nhiều lĩnh vực khác. Hãy đến với dnulib.edu.vn để khám phá thêm nhiều điều thú vị nhé!
Tài liệu tham khảo: https://www.geeksforgeeks.org/dynamic-programming/